ConcurrentSkipListMap详解
介绍:
ConcurrentSkipListMap是线程安全的有序的哈希表,适用于高并发的场景。 ConcurrentSkipListMap和TreeMap,它们虽然都是有序的哈希表。但是,第一,它们的线程安全机制不同,TreeMap是非线程安全的,而ConcurrentSkipListMap是线程安全的。第二,ConcurrentSkipListMap是通过跳表实现的,而TreeMap是通过红黑树实现的。 关于跳表(Skip List),它是平衡树的一种替代的数据结构,但是和红黑树不相同的是,跳表对于树的平衡的实现是基于一种随机化的算法的,这样也就是说跳表的插入和删除的工作是比较简单的。
原理:
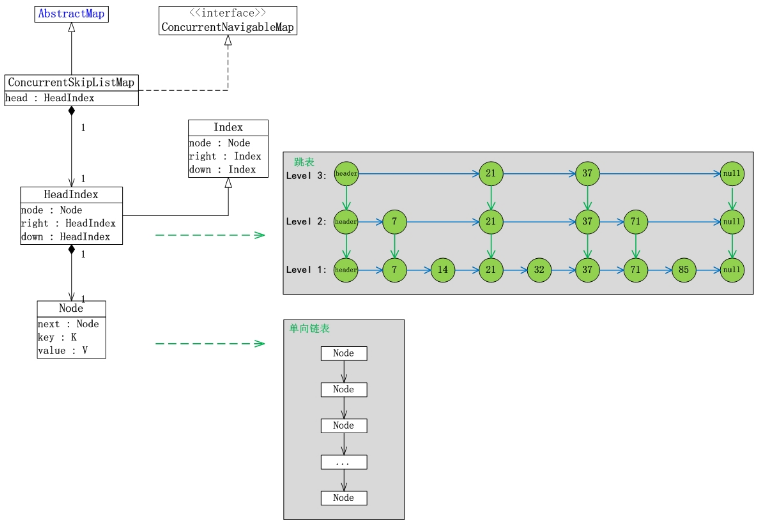
- ConcurrentSkipListMap继承于AbstractMap类,也就意味着它是 一个哈希表。
- Index是ConcurrentSkipListMap的内部类,它与“跳表中的索引 相对应”。HeadIndex继承于Index,ConcurrentSkipListMap中含有一 个HeadIndex的对head,head是“跳表的表头”。
- Index是跳表中的索引,它包含“右索引的指针(right)”,“下索 引的指针(down)”和“哈希表节点node”。node是Node的对象,Node也是ConcurrentSkipListMap中的内部类。
源码分析:
1.添加
public V put(K key, V value) {
if (value == null)
throw new NullPointerException();
return doPut(key, value, false);
}
private V doPut(K kkey, V value, boolean onlyIfAbsent) {
Comparable<? super K> key = comparable(kkey);
for (;;) {
// 找到key的前继节点
Node<K,V> b = findPredecessor(key);
// 设置n为“key的前继节点的后继节点”,即n应该是“插入节点”的“后继节点”
Node<K,V> n = b.next;
for (;;) {
if (n != null) {
Node<K,V> f = n.next;
// 如果两次获得的b.next不是相同的Node,就跳转到”外层for循环“,重新获得b和n后再遍历。
if (n != b.next)
break;
// v是“n的值”
Object v = n.value;
// 当n的值为null(意味着其它线程删除了n);此时删除b的下一个节点,然后跳转到”外层for循环“,重新获得b和n后再遍历。
if (v == null) { // n is deleted n.helpDelete(b, f);
break;
}
// 如果其它线程删除了b;则跳转到”外层for循环“,重新获得b和n后再遍历。
if (v == n || b.value == null) // b is deleted
break;
// 比较key和n.key
int c = key.compareTo(n.key);
if (c > 0) {
b = n;
n = f;
continue;
}
if (c == 0) {
if (onlyIfAbsent || n.casValue(v, value))
return (V)v;
else
break; // restart if lost race to replace value }
// else c < 0; fall through }
// 新建节点(对应是“要插入的键值对”)
Node<K,V> z = new Node<K,V>(kkey, value, n);
// 设置“b的后继节点”为z
if (!b.casNext(n, z))
break; // 多线程情况下,break才可能发生(其它线程对b进行了操作)
// 随机获取一个level
// 然后在“第1层”到“第level层”的链表中都插入新建节点
int level = randomLevel();
if (level > 0)
insertIndex(z, level);
return null;
}
}
}
说明:doPut() 的作用就是将键值对添加到“跳表”中。 要想搞清doPut(),首先要弄清楚它的主干部分 —— 我们先单纯的只考虑“单线程的情况下,将key-value添加到跳表中”,即忽略“多线程相关的内容”。它的流程如下:
-
找到“插入位置”: 即,找到“key的前继节点(b)”和“key的后继节点(n)”;key是要插入节点的键。
-
新建并插入节点: 即,新建节点z(key对应的节点),并将新节点z插入到“跳表”中(设置“b的后继节点为z”,“z的后继节点为n”)。
-
更新跳表: 即,随机获取一个level,然后在“跳表”的第1层~第level层之间,每一层都插入节点z;在第level层之上就不再插入节点了。若level数值大于“跳表的层次”,则新建一层。
2.删除
public V remove(Object key) {
return doRemove(key, null);
}
final V doRemove(Object okey, Object value) {
Comparable<? super K> key = comparable(okey);
for (;;) {
// 找到“key的前继节点”
Node<K,V> b = findPredecessor(key);
// 设置n为“b的后继节点”(即若key存在于“跳表中”,n就是key对应的节点)
Node<K,V> n = b.next;
for (;;) {
if (n == null)
return null;
// f是“当前节点n的后继节点”
Node<K,V> f = n.next;
// 如果两次读取到的“b的后继节点”不同(其它线程操作了该跳表),则返回到“外层for循环”重新遍历。
if (n != b.next) // inconsistent read
break;
// 如果“当前节点n的值”变为null(其它线程操作了该跳表),则返回到“外层for循环”重新遍历。
Object v = n.value;
if (v == null) { // n is deleted n.helpDelete(b, f);
break;
}
// 如果“前继节点b”被删除(其它线程操作了该跳表),则返回到“外层for循环”重新遍历。
if (v == n || b.value == null) // b is deleted
break;
int c = key.compareTo(n.key);
if (c < 0)
return null;
if (c > 0) {
b = n;
n = f;
continue;
}
// 以下是c=0的情况
if (value != null && !value.equals(v))
return null;
// 设置“当前节点n”的值为null
if (!n.casValue(v, null))
break;
// 设置“b的后继节点”为f
if (!n.appendMarker(f) || !b.casNext(n, f))
findNode(key); // Retry via findNode
else {
// 清除“跳表”中每一层的key节点
findPredecessor(key); // Clean index
// 如果“表头的右索引为空”,则将“跳表的层次”-1。
if (head.right == null)
tryReduceLevel();
}
return (V)v;
}
}
}
说明:doRemove()的作用是删除跳表中的节点。 和doPut()一样,我们重点看doRemove()的主干部分,了解主干部分之后,其余部分就非常容易理解了。下面是“单线程的情况下,删除跳表中键值对的步骤”:
-
找到“被删除节点的位置”: 即,找到“key的前继节点(b)”,“key所对应的节点(n)”,“n的后继节点f”;key是要删除节点的键。
-
删除节点: 即,将“key所对应的节点n”从跳表中移除 – 将“b的后继节点”设为“f”!
-
更新跳表: 即,遍历跳表,删除每一层的“key节点”(如果存在的话)。如果删除“key节点”之后,跳表的层次需要-1;则执行相应的操作!
3.获取
public V get(Object key) {
return doGet(key);
}
private V doGet(Object okey) {
Comparable<? super K> key = comparable(okey);
for (;;) {
// 找到“key对应的节点”
Node<K,V> n = findNode(key);
if (n == null)
return null;
Object v = n.value;
if (v != null)
return (V)v;
}
}
private Node<K,V> findNode(Comparable<? super K> key) {
for (;;) {
// 找到key的前继节点
Node<K,V> b = findPredecessor(key);
// 设置n为“b的后继节点”(即若key存在于“跳表中”,n就是key对应的节点)
Node<K,V> n = b.next;
for (;;) {
// 如果“n为null”,则跳转中不存在key对应的节点,直接返回null。
if (n == null)
return null;
Node<K,V> f = n.next;
// 如果两次读取到的“b的后继节点”不同(其它线程操作了该跳表),则返回到“外层for循环”重新遍历。
if (n != b.next) // inconsistent read
break;
Object v = n.value;
// 如果“当前节点n的值”变为null(其它线程操作了该跳表),则返回到“外层for循环”重新遍历。
if (v == null) { // n is deleted n.helpDelete(b, f);
break;
}
if (v == n || b.value == null) // b is deleted
break;
// 若n是当前节点,则返回n。
int c = key.compareTo(n.key);
if (c == 0)
return n;
// 若“节点n的key”小于“key”,则说明跳表中不存在key对应的节点,返回null
if (c < 0)
return null;
// 若“节点n的key”大于“key”,则更新b和n,继续查找。
b = n;
n = f;
}
}
}
所有的操作都使用到了findPredecessor()方法
private Node<K,V> findPredecessor(Comparable<? super K> key) {
if (key == null)
throw new NullPointerException(); // don't postpone errors
for (;;) {
Index<K,V> q = head;
Index<K,V> r = q.right;
for (;;) {
if (r != null) {
Node<K,V> n = r.node;
K k = n.key;
if (n.value == null) {
if (!q.unlink(r))
break; // restart
r = q.right; // reread r
continue;
}
if (key.compareTo(k) > 0) {
q = r;
r = r.right;
continue;
}
}
Index<K,V> d = q.down;
if (d != null) {
q = d;
r = d.right;
} else
return q.node;
}
}
}
说明:从head节点开始查找,先向右查找,如果向右的节点为null或者key小于node.value时就向下查找,最后在level1中查找到key对应的前继节点。也就是说无论是put,remove还是get,最后都会查找到level1的链上,然后再操作。